前回の記事は4章まででしたので、第5章の話をちょこちょこと。

　この章はスイッチを開けたり閉じたりした直後の過渡現象を頑張って微分方程式を立てて解こう！というなかなか過酷な内容になっております。書籍では実は一部数式に誤りがあるところもあり(笑)、悩むところですね。

　最初はこういう微分方程式を解こう、から入るんですが、電気工学科の出身者はそのうち（制御工学等でも出てきていちいちこんなの解いていられないので）ラプラス変換で考えるようになりますが、それは本書では次の章になっております。出現順番としては妥当かな？と思います。

最初の回路の考察

数式立てて解くのは割とやさしい（電圧源も電流源もないから）

　最初に載っている例は割とやさしい話です。コンデンサCに十分電荷が蓄えられている状態でスイッチを時刻t=0で閉じた時コンデンサの両端の電圧vがどのような時間変化をするかというものです。これはキルヒホッフの法則とコンデンサの電荷と静電容量そして電圧との関係で数式立てることができますので。

　まずコンデンサC周りの数式を立てましょうか。スイッチを閉じた後にコンデンサに向かって流れる電流ってすなわちコンデンサに蓄えられた電荷の単位時間当たりの変化量なわけですから、$$i_c = \frac{dq}{dt}$$であって、コンデンサに蓄えられる電荷と静電容量および電圧\(v\)の関係は\(Q=Cv\)なのですから $$i_c = \frac{dq}{dt} = C\frac{dv}{dt}$$ですね。さらに抵抗Rを流れる電流を\(i_R\)とすると抵抗Rの両端の電圧は\(v = i_R \times R\)です( \(v\)はコンデンサ両端の電圧と等しい）。さらにキルヒホッフの法則により$$i_c + i_R = 0$$ですからこれらをまとめれば$$C\frac{dv}{dt} + \frac{v}{CR}= 0$$となるわけで、結果$$ \frac{dv}{dt} + \frac{v}{CR} = 0 \dots (1) $$となります。

微分方程式を解く

　ここで(1)の微分方程式を解きたいわけですが、ちょっと豆知識が出てきてますね。微分したものと微分していない元の\(v\)とを足して0になるということは、左辺としては、微分したものとそのまま足したものがうまいこと相殺されて0になってくれるものということです。ですので、微分しても積分しても形が変わらない（定数倍とかにはなったとしても）ものが答えだよということです。それを満たすのは、高校で微積分習った時に不思議な性質を持った奴がありましたね。\(e^x\)の形式をしたやつですね。ということは(1)の微分方程式の解って、$$v = ke^{st}$$(kとsはまだよくわからないけど、何らかの定数なんでしょう）という形は少なくともしていそうですね。なんか真っ正直に解くのはしんどいじゃないですか。そこで(1)に$$v=ke^{st}$$を代入してみると、$$ske^{st} + \frac{1}{CR}ke^{st} = ke^{st}(s + \frac{1}{CR}) = 0$$という式が得られます。ここで、kは0ではない（それだと\(v=0\)になってしまうので）かつ、\(e^{st}\)はsをどんなに小さくしても0にはならないので、$$s + \frac{1}{CR} = 0$$まで簡略化できて、$$s = -\frac{1}{CR}$$になります。ここでスイッチを開けた時刻t=0では\(v = V_0\)であるとすると、$$V_0 = ke^0 = k $$となるわけで、結果$$v = V_0e^{-\frac{t}{CR}}$$となります。ここまでは割と一直線に解ける話です。CRは時定数なんて言ったりしますね。

電源がある場合の過渡状態

数式は立てられるんだけどね･･･

　ここまでは良いのですが、次は回路に電源が接続されている場合です。載っている回路はこんなやつです。

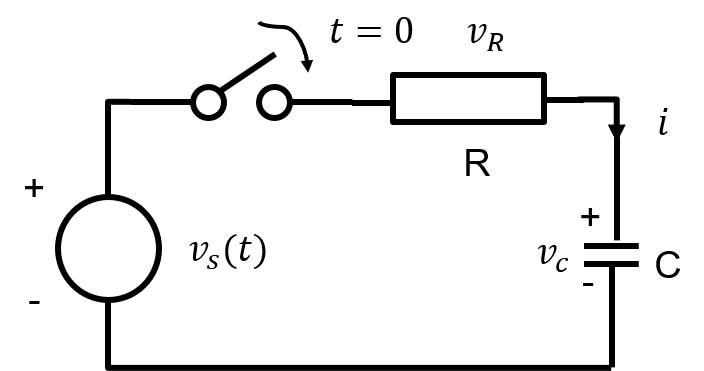
　式の立て方は一緒で、キルヒホッフの法則とコンデンサの性質から、$$v_R + v_C = v_s(t)$$であり$$i=\frac{dq}{dt}=C\frac{dv_c}{dt}$$　$$v_R=R\times i = RC\frac{dv_c}{dt}$$なので、$$RC\frac{dv_c}{dt} + v_c = v_s(t)\dots (2)$$となります。さっきと違うのは右辺に\(v_s(t)\)があることで、これ解くの大変そうです。

未定係数法による解法

　これは解き方として何通りか知られています。上の式は1階の非同次線形微分方程式であり、\(a\frac{dy}{dx}+b=R(x)\)の形で、これは

• \(a\frac{dy}{dx}+b=0\)の一般解
• \(a\frac{dy}{dx}+b=R(x)\)の特殊解（どんなのでもよい。一個見つかりさえすれば･･･）

　の和で表されます。今は1階の非同次線形微分方程式ですが、n階でも同じ事が成り立つので、電気回路の場合2階の微分方程式くらいまでは出てきますが解き方は一緒ということです。未定係数法は、解の形が想像しやすいときにとりあえず解がそれだよと置いてみて微分方程式を解いたときに係数が一意に求まればラッキー、みたいな手法ですね。特殊解の形が予想しやすいなら便利な手法ですが、\(R(x)\)のところは先ほどの回路では\(v_s(t)\)であって、電気回路の場合は定数、\(e^{\alpha t}\)、\(sin\omega t\)とかに限られており（他の交流成分があってもフーリエ級数展開すれば周期のある連続波はsin関数の線形和になるわけだから）、何回微分しても線形倍する数は違えど形が変わらないものなので、未定係数法でやってみよう！というのはとりあえず見通し良さそうですね。まぁいちいち解くの面倒くさいので、そのうちラプラス変換で解析するようにはなりますが、それはこの後で･･･。

特殊解の解き方

　\(RC\frac{dv_c}{dt} + v_c = 0\)の一般解は、前の節の電源のない場合（式（1））なので、$$v_c = ke^{-\frac{t}{RC}}$$の形となります。ここまでは良くて、特殊解の解き方がパターンによって色々だよ、ということです。

\(v_s(t)=V_s\)（定数）の場合

　定数なのだったら、その特殊解Vも定数っぽいですので、そのままV=Aと置いて微分方程式（2）に代入してみます。すると、$$A=V_s$$になりますので一個に求められます。なので、$$v_c=ke^{-\frac{t}{RC}}+V_s$$の形となります。ここで、t=0の時のコンデンサの電圧を\(v_c(0)=V_0\)とすると、$$v_c(0)=k+V_s=V_0$$ですので、$$k=V_0 – V_s$$となって、$$v_c=(V_0 – V_s)e^{-\frac{t}{RC}} + V_s$$が解となります。

　一般に、\(v_s(t)\)が多項式で表される場合、多項式の次数に合わせて特殊解を設定する、というのが定石となっています。定数だったらA, 一次だったら\(Ax+B\),二次だったら\(Ax^2+Bx + C\)と言う具合に置いておく･･･と決まりますね。形を見ると分かりますが、左辺に必ず\(v_c\)の項があるわけでそこで次数が決まっちゃうので\(v_s(t)\)が定数なのに\(v_c\)に一次の項を置いちゃったらその一次の項をどう頑張っても消せない（それより前の項は微分しちゃうので次数が1個下がっちゃうから）から右辺とイコールにできないわけで正しそうですね。それで定数A,B,Cとかを決めちゃうわけです。それが答えです。

\(v_s(t)=e^{\alpha t}\)の場合

　今までのようなやり方で解が求められる場合と、求められない場合とがあります。まぁとりあえず最初は何回微分しても形が変わらないものということで特殊解を\(V=Ae^{\alpha t}\)と置いてみます。（2）に代入すると、$$\alpha ARCe^{\alpha t} + Ae^{\alpha t} = e^{\alpha t}$$なので、$$A(\alpha RC + 1)e^{\alpha t} = e^{\alpha t}$$となるわけですが・・・

\(\alpha RC + 1 \ne 0\)の場合

　これならAが一意に決められるのでそのまま計算できて、\(A = \frac{1}{\alpha RC + 1}\)ってできるのでおめでとうございます。$$v_c=ke^{-\frac{t}{RC}}+\frac{1}{\alpha RC + 1}e^{\alpha t}$$ですね。なので\(v_c(0)=V_0\)とさっきのと同じ初期条件とするんだったら$$v_c=(V_0 – \frac{1}{\alpha RC + 1})e^{-\frac{t}{RC}}+\frac{1}{\alpha RC + 1}e^{\alpha t}=V_0e^{-\frac{t}{RC}}+\frac{e^{\alpha t} – e^{-\frac{t}{RC}}}{1 + \alpha RC}$$という形ですか（計算間違ってたらすみません）

\(\alpha RC +1 = 0\)の場合

　この場合、特殊解を\(V=Ae^{\alpha t}\)と置いてもAが決められないので困りましたね、となります。結論を言うと、この場合は\(V=Ate^{\alpha t}\)という形でも微分したとき形は変わらないので、これを代入するというのが答えになります。本書では、マクローリン展開を用いた求め方を先に載せてますが、まぁ\(\delta << 1\)のときの\(e^{\delta t} \)のマクローリン展開が$$e^{\delta t} = 1 + \frac{\delta t}{1} + \frac{\delta^2 t^2}{2!} + \frac{\delta^3 t^3}{3!}+\dots $$ってのだけ知ってれば分かるかなと。

　では\(V=Ate^{\alpha t}=Ate^{-\frac{t}{RC}}\)を式（2）に代入してみましょう、となるのですが･･･ここで本書、ミスがありまして。代入結果は本当は$$RC(1-\frac{t}{RC})Ae^{-\frac{t}{RC}} + Ate^{-\frac{t}{RC}} = e^{-\frac{t}{RC}}$$ってなるんですよねー･･･（第36版でも直ってませんでした）。結果は合っていて、$$A=\frac{1}{RC}$$と定まるので、$$v_c=V_0e^{-\frac{t}{RC}} + \frac{t}{RC}e^{-\frac{t}{RC}}$$となります。

\(v_s(t) = E_m \sin \omega t \)の場合

　\( \sin \omega t \)の場合は、tで微分すると\(\omega \cos \omega t \)というような形になりますので、cosの項を消せるように特殊解を\(V=A\sin\omega t + B \cos\omega t \) と置いて式（2）に代入してみると、$$RC\omega(A\cos\omega t – B\sin\omega t) + A\sin\omega t + B\cos\omega t = E_m \sin\omega t$$ $$(RC\omega A + B)\cos\omega t – (RC\omega B – A)\sin\omega t = E_m \sin\omega t \dots (3)$$

となります。なので、\(RC\omega A + B = 0, A-RC\omega B = E_m\)ならOKそうですね。ということで、この2つの式から$$A=\frac{E_m}{1 + \omega^2 C^2 R^2}, B = -\frac{\omega CRE_m}{1 + \omega^2 C^2 R^2}$$となります。同じように初期条件を\(v_c(0) = V_0 \) とすると、$$v_c = V_0 + \frac{1}{1 + \omega^2 C^2 R^2} \omega CRE_m e^{-\frac{t}{CR}} + \frac{1}{1 + \omega^2 C^2 R^2}(E_m \sin\omega t – \omega CRE_m \cos\omega t)$$とかって複雑な式となります。書いててあってんのか不安になってきました。

おわりに

　なかなか面倒くさい計算が多いところですが、一応一度は通る必要がある道なので･･･一通り電気回路で使うパターンは書いたつもりです。ちなみに、ここまではコンデンサと抵抗の直列接続のパターンでしたが、コイルと抵抗の直列接続でも原理は一緒です。コイルの場合は電流変化に合わせて逆起電力が生じるので･･･という式になるため、キルヒホッフの電圧則のところが回路を流れる電流をi, インダクタンスをLとすると\(L\frac{di}{dt} + iR = v_s(t)\)の形となり、結局上記の１階の線形微分方程式を解くことになるので、同じ議論ができます。これで本書5.1節の内容は大体カバーできたかなと思います。

　次は２階の線形微分方程式になる場合ですか･･･それは次回、ということで！